核心素养视角下基于高考题的复合型样例设计实践研究

核心素养视角下基于高考题的复合型样例设计实践研究

 杨时喜

腾冲市第六中学      679114

【摘要】本文以2022年高考数学全国乙卷理科17题为出发点，参考复合型样例设计的基本思想，对试题考查的知识点及专家命题意图做出深入剖析，从回归教材的视角探讨高考试题与教材内容的本质联系，并具体回溯到教材相关的例题和习题，揭示了高考试题的命题依托于教材，并以教材的关键例题和习题为生长点的规律；同时对该高考试题的变式进行了尝试性的拓展研究。旨在为高中数学日常教学和高考备考提借鉴和参考。

【关键词】复合型样例设计数学教学高考备考回归教材例题和习题

伴随着中国的不断发展，对人才的培养提出了更高的要求，从客观上推动了新一轮的教育改革，改革的核心是使学生在学习过程中形成真正“素养和能力”，从而将理论与实践更好的结合起来。教育改革的推行，首当其冲的就是课程方案和课程标准的重构和修订，继而是新的教材的编写与推行。高中数学新教材的变革无论从知识网络的重构还是具体内容的编写都发生的很大的变化，重视情境创设和凸显能力培养是最为突出的两个特点。面对新的改革和要求，我们的教学方式和备考策略也必须随之调整和改变。如何调整？如何改变？最有效的方式就是认真研究高考试题的变化趋势和呈现特点，由此来指导自身的教学和备考。下面，我们就从2022年的一道高考数学真题入手，来管窥高考命题的一些变化和特点。

一、真题再现与命题特点剖析

【2022年高考数学全国乙卷理科第17题】

记的内角的对边分别为

已知：.

（1）证明：

（2）若求的周长.

【试题解答】

（1）证明：由题设、三角形的内角和定理及三角函数的诱导公式，得

                          由三角函数和、差角公式得：

同理可得：

由正弦定理得：

（2）解：由（1）知：

 由余弦定理得：

的周长为14.

【试题分析】

本题重点考查正弦定理、余弦定理、三角形内角和定理、三角函数中的两角和差公式等高中数学的基础知识，但对学生的运算求解能力、逻辑思维能力提出了一定程度的要求.同时对学生的学科素养也做了相应的考查。本题的解题路径不唯一，但方法选择不恰当，将增加运算量和得分难度。

第（1）问中，只需根据题设、三解形的内角和定理、三角函数的和差角公式和同角三角函数的平方关系，就可得到三角形三个内角正弦的平方关系，再由正弦定理，代换边角关系，即可得证。如果直接运用三角函数的和差角公式展开的话，需要运用余弦定理的推论进行推，将增加运算量和得分难度。

第（2）问中，给出三角形的一边及对应内角的余弦值，由第（1）问的结论和余弦定理，可得至另外两边的两个关系式，于是可以求出另外两边之和，进而求得的周长。如果学生利用方程思想分别求解，再求周长的话，将会增加运算量和得分难度。

本题看似常规，但在思维要求和细节设计上却颇为讲究，看似给学生更多自由选择的空间，实则在考查学生的学科素养。这里从一定程度上体现了新高考试题的设计特点。

二、探源回溯，回归教材

经过以上的求解分析，我们会发现，2022年高考数学全国乙卷理科第17题涉及的解题能力和核心素养，在教材的相关例题和习题中是有所体现的。现在就让我们回归教材，探寻一下这个题的影子。

高中数学人教A（2019）版必修第二册第42—52页，设计了7个例题，主要用于帮助学生理解正弦定理、余弦定理及其推论的基本应用及适用条件，这是解三角形必备的基础。其中例9—例11，还创设了相关的实用情境，加深学生对正、余弦定理的理解及在现实情境中的应用。这为解决类似2022年高考数学全国乙卷理科第17题这类解三角形的试题奠定了根基。居于篇幅，这里就不在一一列举和分析。

下面侧重来探源一下习题设置中与2022年高考数学全国乙卷理科第17题求解直接相关的几三个题，就其本质而言，2022年高考数学全国乙卷理科第17题就是以这三个题为生长点的。

【人教A（2019）版必修第二册第54页第16题】

在中，求证：

【试题解答】

证明：由余弦定理的推论可得：

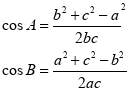
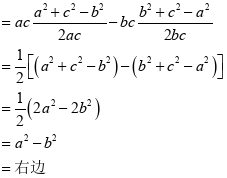
【试题简析】

        这道习题以三角恒等式的证明呈现，主要考查了学生对余弦定理推论的理解和应用，为解与三角形相关的问题奠定了扎实的基础。首先是观察能力，左边是边角混杂，右边是边，所以将左边的角化边，又左边仅有余弦函数名，故采用余弦定理推论完成角化边，继而运算化简即可得证。是解决2022年高考数学全国乙卷理科第17题的必备基础和能力。

【人教A（2019）版必修第二册第54页第17题】

证明：设三角形的外接圆半径是，则

【试题解答】

证明：由题设，所证三个式子结构一致，只需证其中一个即可。

   不妨证其中为的外接圆半径。

          由于三角形可分为锐角三角形、直角三角形和钝角三角形，故分三种情况分别证明

        （1）当为锐角时，如图①所示，作直径连接则在中，

即

（2）当为直角时，如图②所示，在中，可直接得

（3）当为钝角时，如图③所示，作直径连接则在中，

即

           由（1）、（2）、（3）得

           同理可证

【试题简析】

        本题通过证明三角形的边、边所对角的正弦和三角形外接圆三者间的关系，旨在使学生进一步认识和理解正弦定理及其几何意义。但本题却引而不发，做为老师在处理教材时，需进一步引导学生去变形探究，并形成结论。

将本题结论变形可得：隐去其几何意义，

令则有即

令则有即

致此方可让学生具备利用正弦定理进行边角互化的完整基础。继而进行一些运用性训练，为解决类似2022年高考数学全国乙卷理科第17题做好必要的准备。

【人教A（2019）版必修第二册第54页第22题】

已知分别为三个内角的对边，且

（1）求

（2）若则的面积为求

【试题解答】

解：（1）由题设， 根据正弦定理，得

又

即

又

（2）由（1）知

由余弦定理，得

【试题简析】

本题从命题的意图和难度上，已非常接近2022年高考数学全国乙卷理科第17题，所用的知识和技能也比较接近。如果教学时，对本题进行深入剖析和解读，并进行一定的拓展训练，那对于类似2022年高考数学全国乙卷理科第17题这样的题目，失分率将会大大降低。

三、变式拓展，应对变化

2022年高考数学全国乙卷理科第17题侧重证明三边关系和求周长，人教A（2019）版必修第二册第54页第22题则侧重求角及边长，颇有异曲同工之感。然而为了更好的应对试题的变化和考查角度的调整，可在此基础上对以上题目做适当的拓展，譬如将求周长拓展为求周长的范围或求面积等问题。下面就给出两道拓展性试题，以借参考：

【拓展变式一】

在中，设角的对边分别为

已知

求周长的取值范围。

参考答案：

【拓展变式二】

在中，

（1）求的值；

（2）若求的面积.

参考答案：（1） （2）

此处限于篇幅，解答过程从略，仅提供参考答案，由读者自行研究。本质上，拓展的方向和维度还有很多，这时举例一二，只为抛砖引玉之举，大家同行可根据自己的经验和考量自由拓展。

四、复合型样例设计——回归教材的路径之一

以上居于2022年高考数学全国乙卷理科第17题的回溯和拓展，基本上是参考了复合型样例设计的基本思想。经过以上的设计和研究，我们不难发现，高考命题很大程度上仍然植根教材，源于课本，但其变式提高的特征和趋势也非常明显。回归到教材的基础上，还需要多维度的进行拓展训练，对教材的例题和习题进行变式、重组、创新及回溯与拓展，是日常教学与高考备考中，非常值得深入探讨和研究的问题。

【参考文献】

[1]普通高中教科书.数学人教A版.必修.第二册.

[2]2022年高考数学全国乙卷理科试题.

[3]普通高中数学课程标准.北京：人民教育出版社，2017版2020年修订.