（武警警官学院，四川成都 610000）
摘要：本文针对计算对坐标的曲面积分时提供了一种新的解法，有效避免了使用传统方法的繁杂计算，从而提高其计算效率。
关键词：对坐标的曲面积分；向量点积法
一、预备知识
在计算对坐标的曲面积分时，若沿三个坐标轴方向的分量都存在时，即
，
则要分别计算三个积分：
，
，
，因此计算量较大，且不易理解。下面介绍求解对坐标的曲面积分的简便方法，向量点积法。
二、向量点积法
定理：已知曲面
，则
其中：Σ 取上(下)侧，取正(负)号.
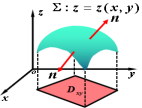
证明：设曲面为
，则可得该曲面的单位法向量为
则有：
故
.
此方法只需要投影到
面，故能提高其计算效率。
三、简单应用
应用1 计算
其中
指向下侧.
解 由题可知，作出曲面
的图，见图1
图1
在
面上的投影区域为
则由向量点积法可得
应用2 计算
，其中是
被平面
所截部分的下侧.
解 由题可知，作出曲面的图，见图2
图2
在面上的投影区域为
则由向量点积法可得
四、结语
综上可知，相对于传统方法求对面积的曲面积分来说，向量点积法求解对面积的曲面积分能简便计算过程，从而有效提高计算效率。
参考文献：
[1]同济大学数学系编,高等数学[M],-7版,北京:高等教育出版社，2014,07.
[2]初颖.对坐标的曲面积分的几种方法[J].学园.2018,12.
客服QQ：30444492琼网文【2021】1550-113号
增值电信业务经营许可证：琼B2-20210322
出版物经营许可证：新出发龙华出字第(2021)009号
广播电视节目制作经营许可证：(琼)字第00779号
版权所有 ©2002-2024 期刊网 琼ICP备2021005105号
