基于时间序列预测的黄河水沙监测数据研究[ 论文来源：2023年“高教社杯”全国大学生数学建模竞赛]

基于时间序列预测的黄河水沙监测数据研究[ 论文来源：2023年“高教社杯”全国大学生数学建模竞赛]

张自豪1，季跃1，王浩1    指导教师：陈杨2

1.山东协和学院 计算机学院，山东 济南250109

2.山东协和学院 基础部，山东 济南 250109

【摘要】研究黄河水沙通量的变化规律对沿黄流域的环境治理、气候变化和人民生活的影响，随着外界因素影响，黄河水沙通量发生变化。根据水利站数据建立合理的数学模型，对黄河水沙监测数据进行分析。本文根据现有黄河水沙通量的基本信息进行数据可视化分析并对缺失数据插值处理，采用线性回归方程分析含沙量与水流量的变化分析，最后列出，乘年数计算出年总水流量和年总排沙量。

【关键词】数据可视化 线性回归方程 插值处理

【中图分类号】TN248.1一、前言

现已知小浪底水库下游黄河某水文站近6年的水位、水流量与含沙量的实际监测数据，由于数据缺失无法简单直观判断出含沙量与时间、水位、水流量的关系，因此可以通过插值处理补充数据，后用线性回归方程分析该水文站黄河水的含沙量与时间、水位、水流量的关系，最后由公式得出年总水流量和年总排沙量。

二、对含沙量与时间、水位、水流量的关系研究

2.1 模型假设

①题目所给的水文站数据准确无误。

②不考虑除题目所给条件以外的其他指标的影响。

2.2 数据可视化

本文根据水利站近6年水位、水流量与含沙量的实际监测数据，分析含沙量与时间、水位、水流量的关系。通过使用软件SPSSPro运行线性回归方程（最小二乘法）来判断2017年水位、水流量对含沙量的之间线性关系的线性系数，通过系数的分析来判别他们之间的相关性。

根据非标准化系数可以得出他们的拟合线性方程为：

    (1)

由该公式可得出拟合优度图：

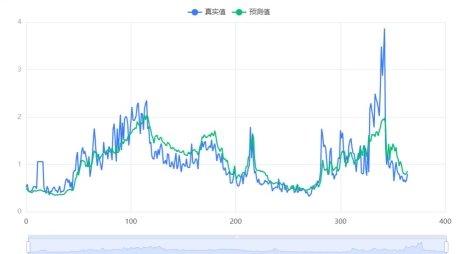
 图 1拟合优度图

上列的的拟合优度图和线性系数表得出，水位、水流量和含沙量的关系呈现线性相关，由热力图验证他们的相关密切性。

图 2热力图

根据剩下2016、2018、2019、2020、2021五年的拟合优度图和线性系数表分别分析，得出拟合优度0514,0421,0.517，0.53,0.621，后根据附录的热力图对相关性密切程度进行检验，由图的皮尔逊相关系数水位与水流量对含沙量的数值接近1，因此可以确定2016、2018、2019,、2020、2021五年的相关性高，最后得出五年的线性公式：

2016年：=-25.294 + 0.002* + 0.601*（i=1）

2018年：=342.868 + 0.013* - 8.162*（i=2）

2019年：=237.588 + 0.009* - 5.646*（i=3）

2020年：=-17.968 + 0.003* + 0.452*（i=4）

2021年：=-112.073 + 2.694*- 0.001*（i=5）

由图中的线性公式及附录中的拟合优度图、线性系数表与热力图，得出：2016、2017、2021年含沙量随水位的上升而上升，2018-2019年含沙量随水位的上升而下降；2016-2020年含沙量随水流量的上升而上升，2021年含沙量随水流量的上升而下降。

2.3 基于含沙量与水位、水流量关系模型的建立与求解

由于附件1中的流量数据为(m3/s)，因此化为小时需乘3600秒，在化为每日天数得到每日水流量，再将每日数据乘每年的天数得到每年水流量，最后得到公式：

                  (1)

根据黄河小浪底调水调沙问题一中提到估计排沙量的方法[1]得出：

排沙量=水流量*含沙量*3600*24

为每天的排沙量化为公式为：

                （2）

2.4结果展示

根据公式(1)和公式(2)分别计算出年总水流量和年总排沙量,如表1、表2所示。

表1 近6年水文站的年总水流量表

表2 近6年水文站的年总排沙量表

三、总结

本文根据现有黄河水沙通量的基本信息进行数据可视化分析，对缺失数据插值处理，后采用线性回归方程分析含沙量与水流量的变化，用最小二乘法验证线性系数，热力图验证相关密切性，最后列出，乘年天数计算出年总水流量和年总排沙量。

参考文献

[1]司守奎  数学建模算法与应用  黄河小浪底调水调沙问题一中提到估计排沙量的方法

论文来源：2023年“高教社杯”全国大学生数学建模竞赛