光伏板倾角对太阳能路灯风荷载特性的影响研究

光伏板倾角对太阳能路灯风荷载特性的影响研究

名字：侯生洲

单位：中国水电四局（兰州）机械装备有限公司 中国水电四局（酒泉）新能源装备有限公司

摘    要：本文采用三维数值模拟方法，研究了光伏板倾角变化对路灯风荷载的影响。结果显示，在斜风向时，升力系数、横风向的基底力矩系数和基底扭矩系数对光伏板倾角变化高度敏感；正面和背面迎风时，阻力系数和顺风向的基底力矩系数最敏感。随着光伏板倾角增大，横风向和顺风向的风荷载最大值逐渐增大，增长速率加快，但基底扭矩系数的最大值无明显增幅。此研究为优化路灯设计提供了理论依据。

关键词：新能源;光伏板;太阳能路灯;数值模拟;风荷载;

在能源短缺和环境污染严重的情况下，开发和利用太阳能等新能源受到世界各国的重视。太阳能路灯不需要电网供电，建设成本低，方便管理和控制，有效减少传统能源消耗，具有高效、节能、环保、低成本等优点。但增加光伏板的倾角，使路灯使风荷载迅速增大，太阳能路灯在沿海地区经常因强风破坏。因此，分析光伏板对路灯风荷载的影响特性，获得太阳能路灯风荷载的计算方法非常重要。本文运用三维数值模拟方法，系统研究了不同倾角的光伏板对路灯风荷载的影响特性，为太阳能路灯设计提供参考。

1 细长塔数值计算方法

1.1 太阳能路灯数值模型

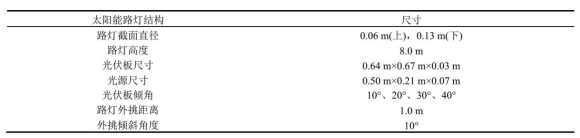
以某地8.0 m的太阳能路灯为研究对象，由于我国南北横跨纬度接近50°南北纬度跨度大，南北横跨纬度接近50°，但大部分面积的纬度在40°以内。为保证光伏板高效率地工作，光伏板的倾角约等于安装地点纬度时，光伏板的发电效率最高。故选取光伏板的倾角α的范围为10°～40°(α=10°、20°、30°、40°)。

表1 路灯各部分细节尺寸 

1.2 计算域及网格划分策略

计算域的选择会影响模拟结果的准确性，通过选取不同尺度的计算域，进行网格无关性验证、算法无关性验证、流域尺度无关性验证，最终确定双流域的混合计算域。计算域的内外流域采用Interface连接，网格划分采用ICEM CFD，外流域进行拓扑分块划分结构网格，内流域划分非结构网格，灯杆、路灯、光伏板近壁面空气流动复杂，在其附近进行二次加密，划分边界层网格。

对无光伏板路灯0°风向下进行网格无关性验证，分别划分了网格量为320万、454万、560万的三套网格，随着网格量的增加，路灯的平均升力系数逐渐趋向于0；平均阻力系数逐渐增加。454万的网格计算出路灯阻力系数与320万的网格计算出路灯平均阻力系数相比增加了10.2%，差别不大，故选取网格量为454万的网格进行后续的计算。

表2 网格无关性验证数据表 

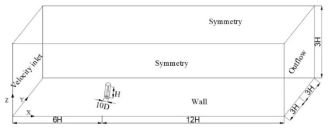
图1 计算域尺寸图  

1.3 数值计算方法及边界条件

全文对太阳能路灯的数值模拟采用SIMPLE算法，选用湍流模型为SST，收敛残差为10-6。具体参数如下表：

表3 三维模型计算参数 

2 数值模拟结果与分析

2.1 光伏板倾角对路灯气动力系数的影响

图2显示了不同倾角光伏板的太阳能路灯平均升力系数CL随风向角变化的曲线。图中数值的正负仅代表方向。曲线关于90°风向呈中心对称，在0°、90°、180°风向时，平均升力系数近似为0，不受光伏板倾角影响；在45°、135°风向时，平均升力系数达到最大值，对光伏板倾角变化最敏感。图3是全风向角下，太阳能路灯平均升力系数最大值随光伏板倾角的变化曲线。随着光伏板倾角的增加，平均升力系数最大值逐渐增大，增长率也逐渐增大。当光伏板倾角为10°时，路灯的平均升力系数略小于无光伏板工况；在20°～40°范围内时，路灯的平均升力系数均大于无光伏板工况；当光伏板倾角为40°时，路灯的平均升力系数最大值达到0.21。

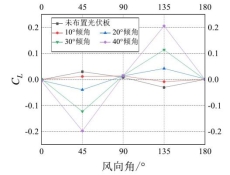
图2 太阳能路灯平均升力系数随风向角变化曲线  

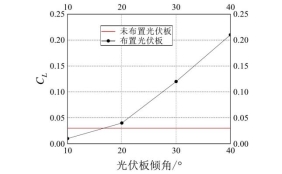
图3太阳能路灯平均升力系数最大值随光伏板倾角变化曲线  

不同倾角光伏板太阳能路灯平均阻力系数CD随风向角变化：图4显示，随着光伏板倾角增加，阻力系数显著增大。曲线关于90°对称。未布置或倾角<10°时，0°-180°范围内先增大后减小，90°最大。20°-40°时，先减小后增大，90°最小，0°、180°最大。

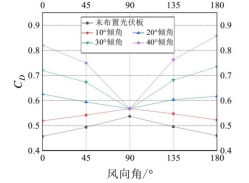
图4 太阳能路灯平均阻力系数随风向角变化曲线  

图5是全风向角下，太阳能路灯平均阻力系数最大值随光伏板倾角的变化曲线。图中未布置光伏板时，路灯的平均阻力系数为0.54，随着光伏板倾角的增加，路灯的平均阻力系数最大值逐渐增加，且增加速率逐渐变大。光伏板倾角为10°～40°时，太阳能路灯的平均阻力系数最大值依次为0.57、0.63、0.73、0.86，相对于未布置光伏板时分别增加了5.6%、16.7%、35.2%、59.3%。

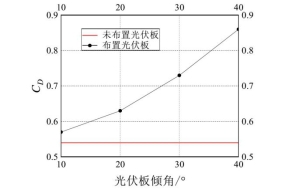
图5 太阳能路灯平均阻力系数最大值随光伏板倾角变化曲线  

2.2 光伏板倾角对路灯平均基底力矩系数的影响

图6展示了不同倾角光伏板的太阳能路灯顺风向平均基底力矩系数CMD随风向角变化曲线。可以看出，太阳能路灯顺风向平均基底力矩系数与太阳能路灯平均阻力系数随风向角的变化趋势一致。此外，基底力矩系数对光伏板倾角的变化十分敏感，随着倾角的增加而显著增大。对于不同的光伏板倾角，基底力矩系数曲线关于90°风向对称。当未布置光伏板或倾角小于10°时，基底力矩系数在0°-180°范围内先增后减，90°风向时达到最大值；而当倾角为20°-40°时，基底力矩系数则先减后增，90°风向时达到最小值，在0°、180°风向达到最大值。

图7展示了全风向角下太阳能路灯顺风向平均基底力矩系数的最大值随光伏板倾角的变化曲线。未布置光伏板路灯的顺风向平均基底力矩系数为0.31，随着光伏板倾角的增加，路灯的顺风向平均基底力矩系数逐渐增加，且增加速率逐渐变大。在光伏板倾角为10°-40°时，太阳能路灯的顺风向平均基底力矩系数的最大值依次为0.34、0.42、0.51、0.66，相对于未布置光伏板时分别增加了9.7%、35.5%、64.5%、112.9%。

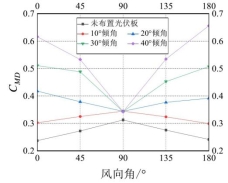
图6 太阳能路灯顺风向平均基底力矩系数随风向角变化曲线  

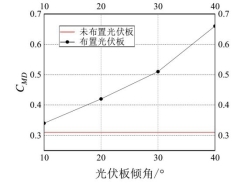
图7太阳能路灯顺风向平均基底力矩系数最大值随光伏板倾角变化曲线  

图8：不同倾角光伏板的太阳能路灯横风向平均基底力矩系数CML随风向角变化曲线，关于90°风向呈中心对称，在0°、90°、180°风向时，系数近似为0；在45°、135°风向时，系数达到最大值，对倾角变化最敏感。

图9：全风向角下，太阳能路灯横风向平均基底力矩系数最大值随光伏板倾角增加逐渐增大，增长率也逐渐增大。

图10：太阳能路灯基底平均扭矩系数CMT随风向角变化曲线，0°和180°风向下基本为0；在0°～180°风向角范围内，先增大后减小，在90°风向时达到最大。

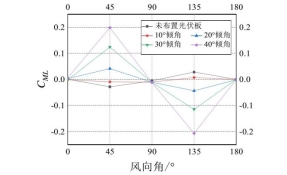
图8 太阳能路灯横风向平均基底力矩系数随风向角变化曲线  

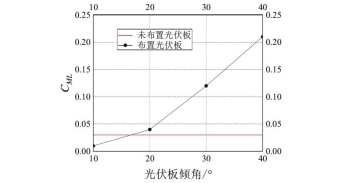
图9 太阳能路灯横风向平均基底力矩系数最大值随光伏板倾角变化曲线  

图11是全风向角下，太阳能路灯的基底平均扭矩系数最大值随光伏板倾角的变化曲线。由图可知，太阳能路灯的基底平均扭矩系数最大值对光伏板倾角的变化不敏感。路灯未布置光伏板时，基底平均扭矩系数最大值为0.80；路灯设置光伏板时，在10°～40°倾角范围内，太阳能路灯的基底平均扭矩系数最大值相对于未布置光伏板工况无明显增幅，最大增加幅度仅为3.8%。

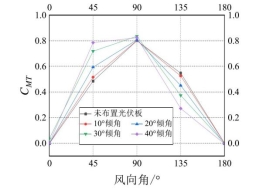
图10 太阳能路灯基底平均扭矩系数随风向角变化曲线  

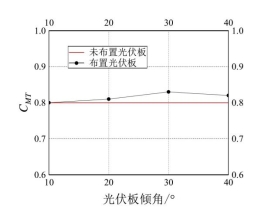
图11 太阳能路灯基底平均扭矩系数最大值随光伏板倾角变化曲线  

2.3 光伏板对路灯风荷载影响机理分析

图12展示了风向为180°时，不同倾角光伏板路灯的流场流线图。图16(a)显示，光伏板对光源流场影响不大，但在灯杆尾流区形成绕流涡。未布置光伏板时，流场在光源壁面流动，中间位置发生边界层分离，但迅速重新附着在光源壁面，未形成明显绕流涡。图16(b)～图16(e)展示了有光伏板时的情况，光伏板前端的下壁面形成绕流涡，倾角越大，绕流涡越大。当倾角为10°和20°时，只在前端形成涡流；当倾角增至30°和40°时，末端下壁面会出现更大的绕流涡，且倾角越大，涡的范围越大。光伏板倾角从10°增加到40°的过程中，阻力系数增加了59.3%。光伏板的倾角对路灯整体平均阻力系数影响较大，应在路灯研究和设计中考虑光伏板的有无和倾角。

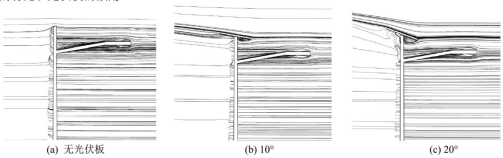
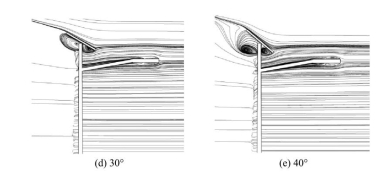
图12 不同倾角光伏板的太阳能路灯流线图 

3 结论

本文运用三维数值模拟方法，研究太阳能路灯风荷载受光伏板倾角的影响，发现不同倾角对路灯的风荷载影响不同，其中升力系数、横风向基底力矩系数和基底扭矩系数对光伏板倾角的变化最敏感。随着光伏板倾角的增加，太阳能路灯横风向和顺风向风荷载的最大值逐渐增大，升力系数的最大值达到0.21，阻力系数的最大值达到0.86。然而，基底扭矩系数的最大值增幅不明显，最大增加幅度仅为3.8%。

参考文献

[1] 李晓诺,王鑫,周达志,陈佳瑜,李茹婷.向日葵式追光智能太阳能路灯设计探讨[J].信息记录材料,2022,23(02):236-239.

[2] 扈志远,王松,王晓阳,何彬,冉绍伯.中国太阳能路灯研究综述[J].绿色科技,2011,(05):195-198.