考虑初始几何缺陷的管桁架稳定性的研究

考虑初始几何缺陷的管桁架稳定性的研究

吴永德  陈宇

中国轻工业南宁设计工程有限公司 广西壮族自治区南宁市 530031

摘要：工程中所有力学问题都是非线性的。静力线性分析所采用的经典力学理论是基于对实际问题简化处理的假定下实现的，如小变形假定、线弹性假定、边界条件不变假定等。若上述假定中任何一种假定不满足，就产生一种非线性现象，若同时不满足多种假定，就会产生多重非线性。

一般力学中的非线性问题包括三类：几何非线性（不满足小变形假定）、材料非线性（不满足线弹性假定）、边界非线性（不满足边界条件不变假定）

关键词：稳定性、非线性、管桁架、大跨度

1.概述

   对于结构通常的线性分析，力的平衡状态是指建模位置上的内力平衡；而对于刚度较柔，变形较大的结构，如大跨空间结构、高耸结构，特别是需要导入预张力的索结构和膜结构，采用线性分析方法会产生较大的误差，甚至得到错误的结果，因此有必要采用几何非线性分析方法计算。

几何非线性分析方法与线性分析方法的主要区别在于：

(1)结构力的平衡位置是结构变形以后的位置，这实际上是考虑我们一般所说的 P-Δ 效应。如图所示，钓了大鱼的钓竿是在其挠曲的位置上平衡的，在挠曲过程中，其内力和挠度关系不再是线性的，而是具有非线性的关系。

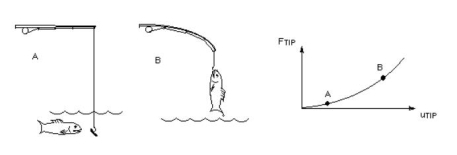
图：钓鱼杆示范几何非线性

(2)单元的刚度不仅考虑结构本身的弹性刚度，而且还需要考虑结构的变形和内力引起的几何刚度矩阵和应力刚度矩阵。

(3)由于力和位移呈非线性关系，所以结构效应（应力、应变、内力和位移等）不能采用叠加原理。

当结构变形产生附加内力达到了必须要考虑的程度（一般认为高耸结构高度超过 60m，大跨结构跨度超过60m，缺陷敏感结构等）应考虑结构的几何非线性效应。

2. 管桁架的特点

管桁架，是指用圆杆（或矩形杆）件在端部相互连接而组成的格构式结构，管桁架作为大跨空间结构的一个分支，广泛应用到各大工程。与传统的开口截面(H型钢)钢桁架相比，管桁架结构截面材料绕中和轴较均匀分布，使截面同时具有良好的抗压和抗弯扭承载能力及较大刚度，因此能利用钢管良好的受力性能和美观的外部造型构成独特的结构体系，满足结构的设计要求，同时这种钢构不用节点板、构造简单、制作安装方便、结构稳定性好。除此之外，管桁架因为屋盖刚度大且钢管壁厚较小、中间空心，因而具有结构自重较轻的优点。

桁架的结构体系一般为平面或空间桁架，在节点处采用杆件直接焊接的相贯节点。对于相贯节点，在同一轴线上的两个主管贯通，其余杆件通过端部相贯线加工后，直接焊接在贯通杆件的外部。目前此类结构多用在机场、体育场和会议中心等公共建筑中。

4.管桁架结构稳定分析的必要性

稳定性分析是管桁架结构设计中的重要环节，鉴于较小的管截面和结构尺寸，局部失稳、平面外失稳和整体失稳都有可能发生。管析架结构多采用分段施工，通过吊装焊接实现整体结构的搭建，考虑到施工精度，焊接和吊装的过程都会使结构产生一定的几何缺陷，特别是对于大跨度结构，因此在管桁架结构稳定性分析中，必须考虑几何缺陷的影响。在钢结构分析中，一般需考虑两种几何缺陷：①构件的初弯曲；②结构的初偏移。

在大跨度结构分析中，缺陷分布模式主要采用一致缺陷模态法和随机缺陷模态法。在一致缺陷模态法中，首先对结构进行线弹性屈曲分析，然后将最低阶屈曲模态（第一阶屈曲模态）乘以比例系数作为结构的几何缺陷，该方法假定结构的最低阶屈曲模态与最终失稳模态相同。在《空间网格结构技术规程》中，规定了需采用一致缺陷模态法对网架结构进行稳定性分析。

5.管桁架几何参数与稳定

(1)桁架的几何参数

立体桁架几何参数示意图一                立体桁架几何参数示意图二

桁架的跨度L指的是结构的在一个方向上两个支撑点的距离，矢高f指的是桁架的起拱高度，桁架宽度b指两根上弦杆之间的距离，桁架高度h指上下弦杆之间的距离。

(2)控制变量

  跨度L=60m，桁架宽度b=2.5m，边界约束：X轴弹性刚度1000kN/mm，Y轴弹性刚度1000kN/mm，Z轴弹性刚度20000kN/mm。

边界条件：

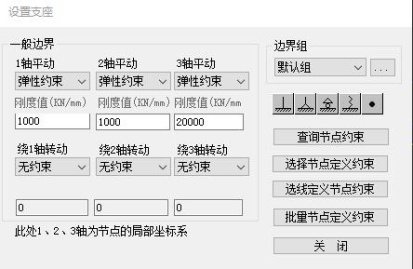
边界条件

(3)稳定分析

在稳定性分析中，首先进行结构的线性屈曲分析，得到模型的屈曲特征值与屈曲模态，然后引入初始几何缺陷对结构进行非线性弹塑性全过程分析，获取结构的失稳模式和稳定承载力。初始几何缺陷最大值按结构跨度的1/300取值进行分析。

非线性屈曲分析比线性屈曲分析更加符合项目的实际情况，用一种逐渐增加荷载的非线性静力分析方法来求得结构失稳破坏时的临界荷载，这种分析方法考虑了加载过程中的变形影响，利用特征屈曲求得的屈曲形状给结构施加初始缺陷。

(4)分析结果

矢高为0m、3m、6m、9m、12m、15m的分析结果如下表：

(5)规律总结

1. 当高跨比h/L固定时，线型稳定系数随着矢高的增加而增加；
2. 当高跨比h/L固定时，非线型稳定系数随着矢高的增加而先增加后减小；
3. 其他条件固定的情况下，矢跨比越大，线型稳定和非线性稳定越好；
4. 矢高为零的情况，其线型稳定系数和非线性稳定系数远小于起拱后（f≠0）的稳定系数；

4.结论分析

(1)当桁架的矢高为零时，其线型稳定系数小于非线性稳定系数。也就是结构在平面外容易失稳，需要设置平面外支撑。

(2)当桁架起拱后（f≠0），其线型稳定系数均大于非线性稳定系数。也就是说结构设计工程中应尽量使用起拱桁架，其稳定性明显高于非起拱桁架。

(3)对立体析架进行平面外稳定分析，得到影响稳定的三个最主要因素:截面的高宽比h/b 、桁架的矢跨比f/L、桁架的高跨比h/L。

(4)当桁架的高宽比h/b=1.0~1.3时，其非线性稳定性最好。当高宽比大于1.3时，结构表现为平面外失稳，此时应增加平面外支撑；当高宽小于1.0时，结构由强度控制。

(5)当桁架的矢跨比f/L＜0.15时，其非线性稳定系数随着跨高比的增大而增大；当桁架的矢跨比f/L>0.15时，其非线性稳定系数不再随着跨高比的增大而增大。工程中应尽量将其高跨比设置在0.15以下。

5.项目应用

(1)工程概况

本工程为体育馆，项目位于南宁市武鸣区，基本风压0.40kN/m2（按100年重现期），抗震设防烈度为6度。采用倒三角空间圆管桁架，桁架钢管之间采用相贯节点，与下部混凝土连接的支座处采用盆式支座，钢材采用Q355B，屈服强度355MPa。

(2)结构布置

屋盖由横向8榀57.4m跨的倒三角空间管桁架作为主要受力构件，纵向由4榀倒三角空间管桁架从檐口和屋架中部贯穿整个横向，增强屋盖的整体性；挑檐部分由4榀平面桁架从柱上悬挑出来，并在平面外设置一平桁架支撑，以减小平面外计算长度；最后延屋盖的四周设置交叉支撑，组成稳定几何不变体系。其具体构成图如下：

       屋盖结构体系构成图                          屋盖三维透视图

(3)设计思路

矢跨比：根据前文的研究对比可知矢高f为零时，其线型稳定系数和非线性稳定系数级差；并且矢跨比f/L＜0.15时非线性稳定系数随着跨高比的增大而增大。因此本工程结合其实际使用需求，将矢高定位4.1m，矢跨比f/L为0.071。

跨高比：当桁架的高宽比h/b=1.0~1.3时，其非线性稳定性最好，故本工程将横向主桁架的高度定为2.6m、宽度定位2.0m，高宽比为h/b=1.3。既达到了最佳的高宽比，又兼顾了建筑功能的要求，使其三角桁架内满足检修走道设置的尺寸要求。

边界条件：纵向桁架支座刚度：Kx=2.607kN/mm，Ky=3.219kN/mm，Kz=2109.38kN/mm；  横向桁架支座刚度：Kx14.346kN/mm，Ky=14.346kN/mm，Kz=3471.43kN/mm；

(4)结果分析

挠度：中部最大位移值132mm，挠度为f=132/57400=1/435，远小于《空间网格结构技术规程》要求的1/250的限值。说明桁架高度取值比较合理。

稳定性：根据《空间网格结构技术规程》，初始几何缺陷取结构的最低阶屈曲模态，并且初始几何缺陷最大值按结构跨度的1/300取值进行分析。规范规定了稳定分析的安全系数K>4.2，本工程采用3D3S对其进行稳定分析。其线型模态如下：

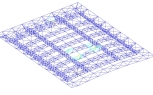
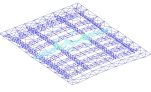
模态一               模态二                  模态三

由图可知，第一屈曲模态（稳定系数为K=17.91）表现为第四榀横向桁架中部平面外局部失稳；第二屈曲模态（稳定系数为K=18.39）表现第五榀横向桁架整体平面外失稳；第三屈曲模态（稳定系数为K=18.84）表现为第三、第四榀横向桁架局部平面外失稳。

如果要解决上述问题，可在横向桁架的中部（屋脊处）布置一道纵向支撑桁架，以增强横向桁架的平面外刚度。但鉴于该模型稳定系数已经达到K=17.91，远大于规范要求的K=4.2的限值，所以具备较大的稳定冗余度。不需要再对比其进行加强。

5.总结

本文以倒三角桁架的稳定性分析（包含线型稳定和非线性稳定）为出发点，通过改变桁架的矢高、桁架的高度等几何参数计算出不同条件下的稳定系数。然后通过对这些数据的分析对比，总结出倒三角桁架合理的矢跨比f/L、高跨比h/L，以及几何参数和稳定系数的变化规律。

将总结出来的研究成果用于指导某大学体育馆空间桁架屋盖的尺寸选型，通过精细化的几何参数对比选取，得出了最优桁架屋面尺寸。并对屋盖进行稳定性分析，验证了研究结果的可靠性，对于后续项目实施具有很好的指导意义。