基于模拟退火粒子群优化算法的子模型组合方式构建信用评分模型

基于模拟退火粒子群优化算法的子模型组合方式构建信用评分模型

黄建建 刘靖明 盛琳腾

上海交通大学苏州人工智能研究院 江苏  苏州  215000

摘要：本研究旨在构建一个高效准确的信用评分模型，以解决金融机构在信贷决策过程中对借款人信用评估的难题。在当前的大数据环境下，借款人的各类信息可以从多个维度进行收集，包括但不限于个人基本信息、征信信息、财务状况、行为特征等。为了充分利用这些信息，本研究采用了一种基于优化粒子群算法的子模型组合方式来构建信用评分模型。首先，我们将收集到的信息分为几个不同的类别，并为每一类信息建立一个逻辑回归子模型，以此来计算各个维度的信用评分。逻辑回归模型因其解释性强、计算效率高而被广泛应用于信用风险评估中。然后，为了得到一个综合的信用评分，我们需要确定这些子模型评分在最终评分中的权重。这里，我们引入了模拟退火粒子群优化算法（Simulated Annealing-Particle Swarm Optimization, SAPSO）来寻找最佳的权重组合，并将此算法与线性回归计算组合权重、基于遗传算法的优化组合权重进行比较。我们在实际数据集上进行了实验验证，通过模拟退火粒子群算法的优化，我们能够找到一组权重，使得组合后的信用评分模型在预测准确性上达到最优。证明了该方法相较于传统单一模型建模方式不仅提高了信用评分的准确性，而且通过子模型的建立，增强了模型对借款人信用状况的解释能力。此外，模型的构建过程考虑了不同信息类型的重要性，使得评分结果更加客观和全面。本研究为信用风险评估领域的研究提供了一种新的模型构建思路，对于金融机构的风险管理和信贷决策具有重要的实践意义和实际应用价值。

关键词：信用评分模型；子模型组合；模拟退火算法；粒子群优化算法；逻辑回归；信用风险评估

1引言

信用评分是金融机构在信贷决策过程中的重要工具，它能够帮助金融机构评估借款人的信用风险，从而决定是否批准贷款以及贷款的条件。随着信息技术的发展，我们可以从多个维度获取借款人的各类信息，如个人基本信息、财务状况、个人征信、行为特征等。这些信息为信用评分模型的构建提供了丰富的数据支持。

传统的信用评分模型通常采用单一模型对借款人的信用状况进行评估，然而，这种单一模型在数据特征空间很大时往往无法充分利用各类信息，且可能忽略了不同信息之间的相互关系；现有的很多个人信用评分模型（如XGBoost、决策树、支持向量机）的单一模型应用效果很大程度上依赖于专家知识和经验去构建，需要通过一定的数据积累和反复实验才能获得理想的模型参数和结构，对于不同产品或场景下需要重复构建多个单一模型耗费成本与时间较高。为了解决这两个问题，本研究提出了一种基于优化粒子群算法的子模型组合方式构建信用评分模型的方法。

本研究的主要贡献在于：首先，我们将借款人的各类信息分为不同的类别，并为每一类信息建立一个逻辑回归子模型，从而能够更准确地捕捉不同信息对信用评分的影响，我们采用粒子群优化算法来确定各子模型评分的最优权重组合，从而形成一个综合信用评分模型，使得预测准确性得到提升；其次，子模型组合方式采用“分而治之”的思想，将一个大的特征空间进行划分成若干个子特征空间，并在每个子特征空间上构造子模型，最后将这些子模型组合起来，这样比在整个特征空间上构造一个单一模型效率更高。通过组合几个结构简单、性能较低的子模型不仅可以取得优于单个复杂分类器的性能，由于组合子模型易于使用且效果良好，即使缺乏模型设计经验的普通操作人员也可以从中受益。最后通过实证分析，我们验证了该方法在信用评分预测准确性上的优势，同时还能够增强模型对借款人信用状况的解释能力。

2模拟退火粒子群算法介绍

粒子群算法（Particle Swarm Optimization, PSO）是一种基于群体智能的优化工具，源于对鸟群捕食行为的研究而发明的进化技术。在PSO算法中，每个粒子代表问题空间中的一个候选解，粒子通过跟踪自己的历史最佳位置和整个群体的最佳位置来调整自己的飞行轨迹，算法通过个体极值和全局最优解的更新来指导搜索过程，最终找到问题的最优解。

模拟退火算法（Simulated Annealing, SA）是一种基于蒙特卡罗思想的优化算法，源于固体材料的物理退火过程。在SA算法中，通过模拟高温金属降温的热力学过程，在搜索空间中寻找目标函数的全局最优解。在算法的每一步的当前温度下，都会随机产生一个新的候选解，并根据Metropolis准则以一定的概率接受或舍弃该解。然后根据预设的退火速度降低温度，进入下一个温度下的迭代，这种策略使得算法能够在搜索过程中跳出局部最优解，从而有可能找到全局最优解。

模拟退火粒子群算法（Simulated Annealing-Particle Swarm Optimization, SAPSO）是一种结合模拟退火和粒子群算法的混合优化方法，它利用模拟退火的概率接受机制来指导粒子群的搜索过程

。在SAPSO中，粒子群算法用于局部搜索，而模拟退火算法用于全局搜索，通过模拟退火算法的概率接受机制，可以在保持粒子群算法快速收敛优点的同时，避免陷入局部最优解，从而提高全局寻优能力和解的质量。在信用评分模型的构建过程中，可以通过SAPSO算法搜索子模型的最佳权重组合，从而提高子模型组合后的预测准确性和泛化能力。

3基于模拟退火粒子群算法的子模型组合方式

3. 1 子模型组合方式的描述

目前国内各大银行的信用评估主要是参考美国的FICO评分体系，其核心是逻辑回归算法，在本文中同样使用逻辑回归算法去构建对应的子模型，逻辑回归具有简单易理解，可解释性强的优点，它的缺点不能很好的处理大量多类特征或变量。为了克服逻辑回归在处理复杂数据时的局限性，我们提出了一种基于模拟退火粒子群算法（SAPSO）的子模型组合方式。这种方式的核心思想是将借款人的信息划分为不同的子类别，并针对每个子类别构建逻辑回归子模型。这样做可以充分利用各类信息的特性，同时避免单一模型在复杂数据空间中的不足。

首先，我们根据借款人的信息特点，如个人基本信息、财务状况、个人征信、行为特征等，将数据划分为多个子类别。每个子类别包含对信用评分有重要影响的相关特征。然后，针对每个子类别，我们构建一个逻辑回归子模型。这些子模型可以独立地学习和预测各自子类别中的信息对信用评分的影响。

接下来，我们利用SAPSO算法来确定这些子模型评分的最优权重组合。SAPSO算法结合了模拟退火算法的全局搜索能力和粒子群算法的局部搜索优势，能够在搜索空间中高效地找到最优解。通过不断调整子模型的权重，我们可以得到一个综合信用评分模型，该模型能够综合考虑各类信息对信用评分的影响，并提升预测的准确性。通过子模型组合的方式，我们可以充分利用各类信息的优势，并在不同子类别之间实现信息的互补。这种方式不仅可以提高信用评分的准确性，还可以增强模型对借款人信用状况的解释能力。通过对子模型的权重进行优化，我们可以进一步提升综合信用评分模型的性能。

3. 2 粒子群算法的编码与适应度选择

粒子群算法采用实数编码 ,一个粒子位置对应于一个可行解。在本文中的模拟退火粒子群算法中，采用的是基于子模型权重系数的编码方式，也就是每个粒子的位置是由D个子模型的权重组成，粒子除了位置之外，还有速度和适应值，为确保子模型权重之和为1，我们通常将粒子位置向量维数设为D-1，所以粒子的速度也应是D-1维向量。

每个粒子的适应度在本文中选取组合后模型的Gini值作为目标函数值。Gini值常用于评估分类模型的性能指标，按每个粒子位置对应的权重去加权组合子模型的预测分数后，然后计算综合分数后模型的Gini值，因为预测是坏客户的违约概率，此时Gini为负值，此时优化权重组合问题即求解最小Gini值，这样个体的适应度与Gini值为负相关，Gini越小，组合模型的分类效果越好，粒子个体的适应度越好。

3. 3 基于模拟退火粒子群算法的子模型组合方式的详细流程

1) 样本数据切分，首先样本数据的特征按不同的类别进行分类划分为多个子样本，每个子样本切片包含样本的样本id、Y标签字段及对应子类别的特征变量Xi。

2) 训练逻辑回归子模型，我们在每个子样本数据上建立逻辑回归模型，根据训练结果获取子模型的预测概率，并将其转换为得分后，将样本所有子模型预测分数及Y标签字段输出到一张宽表中，用于后续的算法适应度计算。

3) 算法参数初始化，设置粒子群大小N，惯性权重最大值wmax，惯性权重最小值wmin，学习因子c1，c2，退火速度β和最大迭代次数M。

4) 生成组合权重问题解域中一个种群，包含N个粒子，随机初始化各个粒子的位置Xid和速度Vi，粒子的位置编码对应子模型权重大小；在本文中粒子位置向量Xid的维度通常为子模型个数D-1，向量每个维度的大小需要限制在0-1之间，对于不满足条件的粒子需要重新生成。

5) 计算每个粒子i的适应度f(x)，f(x)为目标函数，记录每个粒子i的个体最优位置Pid、全局最优位置pgd、适应度f(Pid)和全局最优适应度f(Pgd)。

6) 根据全局最优适应度f(Pgd)计算得到退火算法的初始温度T，计算方式如下：

7) 计算当前温度下每个粒子的退火算法适应度fsa(Pid)，fsa(Pid)为退火算法适应度的函数，计算方式如下：

8) 采用轮盘赌选择算法的思想，从个体最优位置Pid中选择一个粒子位置记为Prd，轮盘赌选择方式是选择算子的一种，又称为比例选择方法，主要思想是：用概率的方法将种群中适应度良好的个体选出，各个个体适应度越好被选择的概率越高。上面退火算法适应度fsa(Pid)的计算公式可以看出，个体最优位置Pid的适应度越好对应的退火算法适应度值fsa(Pid)越大。每次通过获取一个0到1的随机数pBet，根据退火算法适应度值fsa(Pid)计算累计概率

comfit(j)，其公式如下：

根据累计概率，选择用满足条件：的第r个粒子的个体最优位置标记为Prd。

9) 将粒子群公式中的全局最优位置替换为通过轮盘赌选择出来个体最优位置Prd，对速度更新公式中惯性权重因子ω做出如下改进：随着叠代进行，ω由最大惯性权重因子wmax减少到最小惯性权重因子wmin，带入公式后，更新各粒子的速度和位置如下：

10) 再计算各个粒子的适应度，更新各个粒子的最优位置Pid和全局最优位置pgd，通过比较粒子Xid的适应度值和它经历过的最好位置Pid的适应度值，如果更好则更新Pid；比较粒子Xid的适应度值和群体所经历过的最好位置Pgd的适应度值，如果更好则更新Pgd。

11) 进行退火操作，更新温度值，公式如下：

12) 判断是否满足初始设置的终止条件，如果满足结束算法；如果未满足，返回第7步，继续执行7-11步，直至满足终止条件为止。

综上所述，基于模拟退火粒子群算法的子模型组合方式的主要流程如下图1所示：

图1子模型组合建模流程图

算法的具体实现如下：

Begin

Initialize

输入子模型个数D,设置粒子群体大小N,惯性权重最大值wmax,惯性权重最小值wmin,学习因子c1、c2,退火速度β和最大迭代次数M；

for i=1 to N

            for j=1 to D-1

X(i,j) = rand();

V(i,j) = rand();

end

end

计算粒子群中个体的适应度,及粒子个体最优位置Pid和全局最优位置pgd;

计算初始温度T；

for t=1 to M

计算当前温度粒子退火适应度Tfit;

  pBet = rand();

  for i=1 to N

    ComFit(i) = sum(Tfit(i));

    if pBet <= ComFit(i)

Prd=X(i,:);

      break;

    end

  end

粒子速度更新;粒子位置更新;

if 粒子适应度 > Pid的适应值

更新 Pid

end

if 粒子适应度 > Pgd的适应值

　　　  更新 Pgd

end

T = T * β;

end for

输出历代最优个体

End

4 实验结果

采用国内某金融机构真实数据作研究样本集，主要采集了用户的个人人行征信数据等，经过脱敏处理后形成样本数据集。在对数据进行建模之前，需要对数据进行特征工程，使用相关自动特征算法分别生成4类特征子类别：征信贷款账户信息特征、征信信用卡账户信息特征、征信担保信息、征信查询信息特征。根据这4个不同类别的特征构建4个逻辑回归子模型，将子模型预测值与样本真实值组成新的样本集，分别采用线性回归算法、遗传算法和模拟退火粒子群算法计算组合权重系数，将算法得到的权重系数去组合子模型预测分得到综合分数，在样本上计算Gini值和KS值。同时在全部特征上构建一个单一逻辑回归模型作为参照。在本次实验中，设置遗传算法和模拟退火粒子群算法的种群大小N均为100，迭代次数设置为1000，实验结果为表1所示，图2给出了遗传算法和模拟退火粒子群算法算法在迭代过程中，每代群体中最佳个体的适应度值。

表1 实验结果

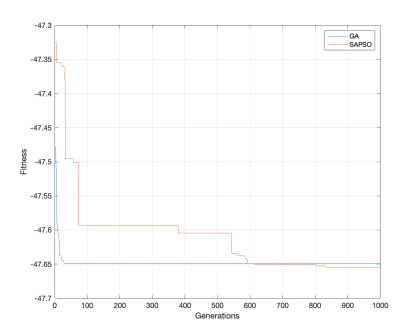
图2收敛曲线对比图

实验表明，在同样的特征空间下，子模型组合的构建方式比单一模型建模方式预测准确度更高；本文的基于模拟退火粒子群算法的子模型组合方式的全局寻优能力和解的质量高于基于线性回归模型子模型组合和基于遗传算法子模型组合。

5 结论

基于模拟退火粒子群算法的子模型组合方式，形成一个综合信用评分模型，可以使得模型的预测准确性得到提升，而且通过组合几个逻辑回归的子模型的方式保证了模型的可解释性。同时子模型的组合方式可以节省后续模型构建或迭代的成本与时间，在新增子类特征上构建其他子模型然后重新组合新的综合评分模型即可。

参考文献:

[1]刘靖明,韩丽川.粒子群优化k均值的混合聚类算法研究[J].中国管理科学,2005:96-99.

[2]个人信用评分与信用卡风险控制研究[D].吉林大学,2006.

[3]向晖,杨胜刚.个人信用评分关键技术研究的新进展[J].财经理论与实践,2011:22-26.

[4]石庆焱,靳云汇.多种个人信用评分模型在中国应用的比较研究[J].统计研究,2004:43-47.

[5]个人信用评分组合模型研究与应用[D].湖南大学,2011.

[6]组合评价模型的研究与应用[D].兰州大学,2007.

[7]高鹰,谢胜利.基于模拟退火的粒子群优化算法[J].计算机工程与应用,2004:47-50.