二次函数的图象在解题中的应用研究

二次函数的图象在解题中的应用研究

姓名：温新斗

单位：广东省高州市石龙中学邮编：525241

摘要：二次函数相关知识概念，是我国初中阶段数学学科之中的关键知识内容，也是初中阶段数学学科之中的难点之一，初中生需要掌握二次函数的图象性质，同时可以做到利用二次函数图象，解决实际的数学问题，换而言之，就是初中生必须掌握应用二次函数相关图象的正确方法。基于此，本文对我国初中阶段二次函数相关教学进行分析，给出数学教师引导初中生准确应用二次函数图象，需要运用的一系列教学策略。

关键词：初中教育；数学教学；二次函数；函数图象；应用策略

前言：在初中阶段的各学科教育工作之中，数学学科占据着关键地位，二次函数为九年级初中生学习的数学知识，由于该知识内容存在一定的复杂性和抽象性，这使得初中生在学习二次函数的过程中，很容易产生解题思路混乱、找不到明确解题路径等问题。针对这一情况，数学教师需要为初中生传授应用二次函数图象的解题方法，通过多种教学策略帮助初中生真正理解和掌握相关知识，从而帮助初中生扫除解题障碍，促进初中生在学习道路上持续进步。

一、二次函数相关内涵分析

函数的定义域属于实数集，而且在函数的表达公式之中，含有二次项的函数，就是二次函数。二次函数的一般形式为f(x)=ax2+bx +c(a≠0)，在此之中，a、b、c三者均为实数，a就是二次函数之中的二次项系数。二次函数相关的图象，通常为呈现出“U”型的曲线，也被称为抛物线，在二次函数之中包括顶点坐标、对称轴、零点、开口方向等要素。

在绘制二次函数图象时，通常会运用点草图法，该方法又被称为“五点作图法”，目前在初中阶段数学教学之中得到运用。在二次函数的图象内部包括五个点，这五个点同等重要、缺一不可，包括顶点、与x轴的交点、与y轴的交点和对称轴相关的两个对称点。需要注意一点，虽然绘制图象的方法被称为“点草图”，实际上绘制完成的图象并非草图[1]。

二、初中生在解题过程中应用二次函数图象的策略

（一）应用二次函数图象明确不同数值的大小

初中生要想对不同数值的大小进行比较，可以运用二次函数的图象，在此类问题之中，包含的数值通常为点坐标值，在比较大小的过程中，可以运用以下两种思路：（1）对不同点的相关位置关系进行充分利用；（2）通过作差的方式，对不同数值之间的大小关系进行直接分析。

例题1：已知抛物线y=x2+2x-3，与x轴的负半轴在点A相交，同时与y轴在点B相交，直线m同时经过点A和点B。（1）求直线m的函数表达式。（2）如果点P（a，y1）和点Q（a，y2）分别为抛物线以及直线m上面的两个点，而且-3＜a＜0，请判断y1与y2的大小，并说出判断大小的理由。

数学教师带领初中生对该题目进行分析，会发现该题目属于综合的二次函数题目，初中生在解题过程中，需要关注不同点所在的位置，运用数值作差进行分析，最终给出准确的判断，明确不同数值的大小。

例题1的解题思路：（1）根据题目给出的y=x2+2x-3可以得知，y=（x+3）（x-1），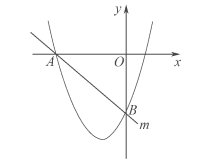
抛物线与x轴的交点坐标为（-3,0）以及（1,0）,在对函数图象（见图1）进行分析之后，点A的坐标为（-3,0），点B的坐标为（0，-3）。直线m的解析式可以被设置为y=kx-3，代入A点之后获得k=-1，因此直线m的表达式为y=-x-3。（2）已知点P（a，y1）和点Q（a，y2），分别为抛物线以及直线m上面的两个点，因此y1=a2+2a-3，y2=-a-3，所以y1-y2=a（a+3）。由于题目当中已经给出条件-3＜a＜0，所以得出结论y1＜y2。

图1 例题1的二次函数图象

（二）应用二次函数图象的平移知识完成解题

部分初中生虽然可以掌握二次函数图象的应用方法，但如果二次函数图象出现了平移情况，此类初中生可能会出现思路混乱的情况，因此在实际解题过程中，必须深入了解图象平移的情况，在真正掌握知识的基础上，通过平移得到题目的正确答案[2]。

例题2：二次函数y=-2x2+4x+1的图象如何进行平移，才能够获得函数y=-2x2的图象（）。

A.先将图像向左平移1个单位，然后向上平移3个单位

B.先将图像向右平移1个单位，然后向上平移3个单位

C.先将图像向左平移1个单位，然后向下平移3个单位

D.先将图像向右平移1个单位，然后向下平移3个单位

例题2的解题思路：在解决图象平移题目时，初中生需要将二次函数相关解析式，转变为二次函数相关的顶点式，然后利用配方的方法，对平移需要选择的方向、单位进行确认。题目已经给出二次函数原本的解析式，因此需要进行转化，转化之后的解析式为y=-2x2+4x+1=-2（x-1）2+3，由此可见，图象需要向左侧平移1个单位，然后再向下平移3个单位，才能够将原本的函数图象，转变为函数y=-2x2的图象。

由此可见，在对二次函数图象进行平移的过程中，初中生需要做到透过现象观察本质，平移的本质就是图象的顶点出现变化，因此初中生必须将已有的解析式，转化为直观的顶点式，找到准确的顶点坐标，然后根据“上加下减，左加右减”的解题原则，完成平移并且利用解题求得正确答案。

三、应用二次函数相关图象进行解题的反思

首先，数学教师需要关注初中生是否了解抛物线的开口方向。初中生不得急于解题，而是需要提前观察二次函数的系数a是正数还是复数，然后对图象的抛物线开口进行确认。如果a＞0，说明图象抛物线有着向上的开口；但如果a＜0，就说明图象抛物线有着向下的开口。这种判断图象的方法，在性质判断方面大有用处，而且二次函数方程的变形，也需要对抛物线的开口进行精准判断。

其次，数学教师需要帮助初中生了解图象的对称轴。二次函数相关图象之中的对称轴，就是在抛物线中心位置划出的一条线，要想获取对称轴的方程，初中生需要将二次函数之中的x转变为-x。不仅如此，初中生在利用图象解决二次函数问题的过程中，必须利用对称轴明确二次函数所具备的对称性。

再次，二次函数图象之中的“零点”，就是函数值为0的坐标x，初中生在运用图象解题时，可以根据实际情况利用零点，对二次函数的交点进行确认，从而明确解决问题的正确思路[3]。

最后，数学教师需要引导初中生综合运用图象。运用二次函数的相关图象解决实际问题，并非对单一概念、公式的运用，而是需要初中生根据不同的题目，灵活运用多种解决问题的策略，例如对图象进行绘制并且全面观察等，从而找到最适合的问题解决方法，不得机械地套用已经学习的图象知识。

结论：综上所述，二次函数由于存在一定的难度，因此初中生在进入九年级时才能够接触，尽管九年级的初中生已经积累了一定的数学学习基础，但是二次函数题目仍旧会对初中生造成困扰。所以初中阶段的数学教师必须积极行动，通过课堂教学引导初中生利用二次函数的图象完成解题，帮助初中生真正掌握相关知识。

参考文献：

[1]郑子飚.初中数学解题方法和技巧研究——以二次函数解析式为例[J].新课程导学,2023,(14):56-59.

[2]张洋.数形结合在二次函数图象解题教学中的应用[J].中国多媒体与网络教学学报(下旬刊),2021,(07):50-51+93.

[3]佟丽.自主探究规律提高思维效能——“与二次函数图象有关的结论判断”一课的教学及反思[J].理科考试研究,2024,31(10):20-24.