函数图像中的角的存在性问题

函数图像中的角的存在性问题

邱忠娟 

重庆实验外国语学校 400051

摘要：函数图像中的45°角存在性问题是今年的新考点，问题突破的关键是结合条件和图形特征，合理添加辅助线，便能快速获得解决问题的途径，下面将剖析问题背景，结合实例具体讲解四种构造策略，并进行方法总结，提出教学建议.

关键词：45°角；解法；等腰直角三角形；模型；辅助圆

在重庆中考数学中，以二次函数为背景的角度问题是今年的新考点，尤其是解答题中的45度角的存在性问题，题型新颖，使不少同学犯难.这类问题不仅在思维层面上对学生有一定要求，而且对学生的计算能力要求也很高.接下来，我们将给出函数图像中的45°角的存在性问题的通性通法.

提出问题

在平面直角坐标系中,存在定点A（a，b）、B（c，d）,在函数的图像上存在动点P（m，f(m)）,那么当时，求P点的坐标.

解题模型

针对以上问题，我们通常有以下四种解题方法.

法一：构造“一线三垂直”模型

如图1：

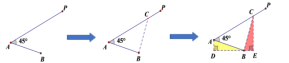
图1

这里选择以B为直角顶点构造直角三角形，是因为有更多的已知信息，为题目提供了更多有用的条件。从而可建立方程组：

解方程组求出点C的坐标为（x，y）,根据A、C两点坐标求出直线AP的解析式，再和函数联立方程组，即可求出P点的坐标.

法二：“12345”模型

如图2：

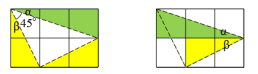
图2

具体为：，这三个量知二推一.

法三：辅助圆

如图3,当时，可看成B、P、A共圆，即弧BA所对的圆心角为90°，根据图形找到圆心和半径，从而求出点P的坐标.

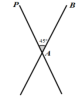
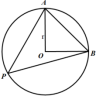
图3                    图4

法四：夹角公式

如图4，直线AB与直线PA所形成的最小正角为45°,则

从而求出,根据待定系数法求出AP的解析式，再和函数联立方程组，即可求出P点的坐标.

接下来，让我们一起通过例题来加强对方法的理解.

例1  如图，抛物线经过点,且交x轴于A(-6，0）,B两点（点A在点B的左侧）,交y轴于点C.

（1）求抛物线的解析式.

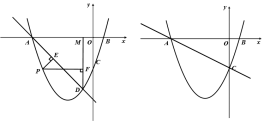
（2）如图1，过点D作DM⊥x轴，垂足为M，点P在直线AD下方抛物线上运动，过点P作PE⊥AD,PF⊥DM，求的最大值，以及此时点P的坐标.

（3）将抛物线沿射线CA方向平移个单位长度，在平移后的抛物线上存在点G，使得，请写出所有符合条件的点G的横坐标，并写出其中一个的求解过程.

解  (1)(2)略

(3)易知平移后的抛物线的解析式

法一：如图5，当点G在直线AC上方时，以C为直角顶点构造等腰直角三角形ACT， 过点C作直线PQ∥x轴，分别过点A、T，作AP⊥PQ交于点P，TQ⊥PQ交于点Q.可得：.

所以,设则有：解得：.

即.从而求出AT：.联立方程组,求出.

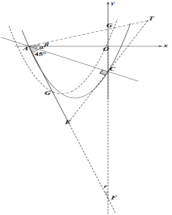同理当点G在直线AC下方时，求出.

　图5

法二：如图6，当点G在直线AC上方时，因为则.

从而求出AT：.即可求出点G的坐标，答案同上，当点G在直线AC下方时，同理可得.

图6

法三：因为直线AC和直线AT所形成的夹角为45°，且.所以.解得：.后面过程同法一.

变式：在原抛物线上，顶点为A，和点,在直线上是否存在点G，使得若存在，请求出点G的坐标.

解：由题意得：.因为.所以.即A、B、G三点在以O为顶点，OA为半径的圆上，如图7，此时半径.从而求出.

图7

总结反思

新课标提出的9大核心素养之一：数学模型的建立与应用，是指学生能够运用数学概念、知识和方法构建数学模型，并运用模型进行问题的分析和求解，培养建模思维和问题求解的能力。在以上的例题中,由45°角自然联想等腰直角三角形，法一是通过"横平竖直辅助线"构造一线三垂直模型，法二是45°的特殊情况：12345模型，法三是引入了夹角公式，当发现角的顶点未知时，常常借助辅助圆可快速求解．

在日常教学中，我们可以通过题目解构、基本图形和例题的回顾、鼓励多角度思考、设置变式练习、鼓励尝试和创新等教学策略的实施，让学生可以逐渐意识到平时做过的例习题或总结的基本图形等是解题的重要工具，并学会在解题过程中细细琢磨其结构、反思其用途与变化、勇于尝试新的方法。这将有助于他们找到解题的金钥匙，提高他们的解题能力和思维能力．