“品字图”——构建分量与总量关系的桥梁 

“品字图”——构建分量与总量关系的桥梁 

刘宸

南京市西善花苑小学，江苏 南京 210012

模型意识主要是指对数学模型普适性的初步感悟。知道数学模型可以用来解决一类问题,是数学应用的基本途径。新课标中认为，数学模型搭建了数学与生活的桥梁，培养模型意识是学生体会数学与外部世界联系的基本途径。教学中应努力创设真实情境，鼓励学生从具体情境中抽象出数学问题，并尝试用数学的知识和方法求出结果。在此基础上，可以回到现实情境中检验并解释结果的实际意义。

苏教版小学数学一年级下册《求减数的简单实际问题》一课主要内容是解决问题，过去的小学数学教材把解决问题部分单拎出来教学，叫做“应用题”，如今苏教版教材中把解决问题穿插在认数和计算中进行教学，客观上削弱了解决问题本固有的逻辑联系，造成学生学习、掌握解决问题知识出现断痕。一年级学生阅读水平低，理解能力弱，生活经验缺失，加上教材原因，解决问题这一题型一直是他们的学习难点。他们不能从解决问题内在本质的程度上去思考，解题往往凭经验。他们不能建构数量关系，不能建构知识间的联系。基于此，笔者在以这节课准备一节公开课时，进行了一些思考和实践，依托品字图学具，着力让学生经历分量与总量数量关系模型的建立，培养学生的模型意识。

【教学片段】

一、基本训练，复习“品”字图

(一) 复习“品字图”。

谈话：同学们，还记得我们的老朋友吗？

展示“品”字图

谈话：如果我在“品”字图里填上数字，使其成为分与合，谁会说？

预设：8可以分成5和3，5和3合成8.

出示倒“品”字图。

预设：3和5合成8，8可以分成5和3。

明确：这是我们学过的“品”字图和倒“品”字图。

追问：这里的8在分与合中表示什么？

追问：这里的3和5在“品”字图里表示什么？

明确：根据分与合，我们知道部分数+部分数=总数（板书）、总数-部分数=部分数（板书）

（二）用“品字图”摆数量关系。

谈话：“品字图”在解决问题中叫做关系图,它能帮助我们分析数量关系。

出示加法题：吃了20个桃，还剩7个，原来有多少个桃？

提问：你能用关系图摆出它们的数量关系吗？

明确：是的，这道题是关于部分数+部分数=总数。

出示减法题：摘了28个桃，吃了20个。还剩多少个桃？

提问：这道题，你会摆成关系图吗？

明确：是的，这道题是关于总数-部分数=部分数的。

二、操作感悟，探索新知

（一）例题  摆一摆关系图，再列式解答。

谈话：关系图好用吗？今天我们还用关系图继续学习解决问题。瞧，猴妈妈和小猴又在果园里摘桃子吃。

出示例图。

提问：读一读图片中的条件和问题。

追问：在这里28个桃表示什么意思？

活动要求：

1.读一读，说出条件和问题。

2.摆一摆，摆出关系图，知道怎样求出问题。

1）摆一摆

2）贴一贴

3）理一理

4）说一说

找学生作品上黑板展示，保留正“品”字图。

明确：可以把一共摘的28个桃分成已经吃掉的和还剩下的两部分，在这里求的是吃了的部分，用减法计算。

3.算一算，写出算式并口答。

（二）练习1：摆一摆关系图，再列式解答。

活动要求：

1.读一读，说出条件和问题。

2.摆一摆，摆出关系图，知道怎样求出问题。

3.算一算，写出算式并口答。

拍照投影

提问:例题和练习1进行比较，有什么相同点？

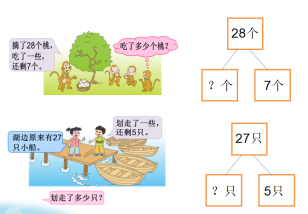
相同点：都是求部分数，对照板贴（总数-部分数=部分数）

明确：是的，都是求部分数，用减法计算。

提问：再和复习题减法题进行比较，有什么不同点？

复习题是：原来-用去=剩下

明确：这道题是知道原来，知道剩下，求用去多少，原来-剩下=用去。

出示课题：《求减数的简单实际问题》

三、举一反三，巩固深化

（一）练习2：先画关系图，再列式解答。

谈话：刚刚我们摆了关系图，那关系图你会画吗？想不想试一试。在脑中想一想关系图，再把它画出来，并列式计算。

总结:这节课我们学了什么？学会了什么？

（二）练习3：想一想关系图，再列式解答。

谈话：我们今天学的内容和之前学的内容是有联系的，有怎样的联系呢？下面让我们来做一组练习。

谈话：同学们，我们不再摆图了，我们现在想图，一边想，一边计算。

1．小猴摘了8个桃子，树上还剩20个，树上原来有多少个桃子？

2．树上原来有28个桃子，现在还剩20个，摘了多少个桃子？

3．树上原来有28个桃子，摘了8个桃子，现在还剩多少个桃子？

回答分2个层次：

1.每一道题头脑中有关系图，说清关系式。

2.追问：为什么第一题用加法列式计算，第二题和第三题用减法列式计算？

明确：都是总数和部分数的关系。

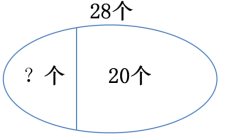
谈话：除了用“品”字图，我们还能用一个椭圆来表示这三道题的数量关系。

小结：我们可以摆、画关系图，用关系式解决部分数+部分数=总数、总数-部分数=部分数这一类题目。

（三）练习4：编题

谈话：我们刚才用关系图帮我们解决了实际问题，我们还可以利用关系图帮我们编题，你们会吗？根据算式，摆“品”字图，编一道类似例题的实际问题。

活动要求：

1.想一想，根据算式想出一道类似例题的实际   问题。

2.摆一摆，摆出关系图。

3.说一说，和同桌相互说一说编的题目。

【教学思考】

数学模型是为了某种目的，用字母、数学及其他数学符号建立起来的等式或不等式以及图表、图像、框图等描述客观事物的特征及其内在联系的数学结构表达式，它可以用来解决一类问题。在本节课中，三种解决问题的数量关系说起来比较复杂，但如果借助品字图帮助分析数量关系，学生就会建立关于三种问题数量关系的模型。那么在本节课中，笔者是如何帮助学生建立模型，发展学生的模型意识呢？笔者认为主要体现在以下几方面：

一、借助品字图，建立分量与总量的模型

品字图来自于教材的“分与合”，将分与合中的数字褪去，抽象出来用符号表示，就能得到品字图（图1）。品字图在解决问题中，又叫做关系图，“合”的部分表示总量，“分”的部分表示分量。例题教学中，学生把摆的关系图贴在黑板上。教师和学生一起理黑板上的作品，把错误的去掉，重复的去掉，最后剩下一张关系图（图2）。学生根据关系图说数量关系：要想求吃了多少个桃，就要从摘了的8个桃中去掉剩下的7个桃，求的是分量，用减法计算。借助品字图，通过摆一摆、贴一贴、理一理、说一说，学生建立求减数的实际问题的数量关系的模型。

           图1

                                          图2

二、经历三次操作：摆图、画图、想图，内化模型

一年级学生的思维以直观形象为主，教学中引导学生通过操作活动把新知识内化到自己的认知结构中。因此例题的处理，我们安排了摆品字图的活动，接着为了巩固学生用品字图分析数量关系的技能，想想做做第1题（图3），我们再次安排学生摆品字图分析数量关系。但学生的思维，不能一直停留在直观，还需要有思维的进阶。想想做做2（图4），我们安排学生画关系图。这对学生思维的要求更高，是从直观到抽象。最后，我们安排一个题组：1．小猴摘了8个桃子，树上还剩20个，树上原来有多少个桃子？2．树上原来有28个桃子，现在还剩20个，摘了多少个桃子？3．树上原来有28个桃子，摘了8个桃子，现在还剩多少个桃子？对学生的要求是在头脑里先想图，再列式解答，学生的思维从抽象到想象。这节课，学生经历摆图、画图、想图，思维从直观到抽象再到想象，内化模型。

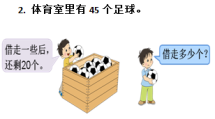
（图3）                            （图4）

三、比较深化，体会三类问题的联系与区别

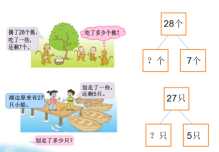
比较，是认识事物之间相同点和不同点的一种思维方法。这节课“求减数的简单实际问题”与第一课时的“求被减数的简单实际问题”以及之前学的“求差实际问题”需要放在一起进行比较，通过比较，学生体会三种解决问题的联系与区别，从而建立分量与总量实际问题的三种模型，求分量用减法，求总量用加法。想想做做第一题教学完毕后，教师把例题与想想做做第一题放在一起比较（图5），明确这两道题虽然问题情境不一样，但求的都是分量，用减法计算。然后把例题与复习品字图环节的练习题放在一起比较（图6），之前学习的数量关系是原来-用去=剩下，“求减数的实际问题”的关系图中，问号在左边，是知道原来，知道剩下，求用去多少，数量关系是原来-剩下=用去，虽然它们求的都是分量，但数量关系不一样。

图5                                  图6

解决问题是学生学习数学的一个难点，我们可以通过建立数量关系的模型，让抽象的知识简单化，而这也是数学应用的基本途径，更是立足学生核心素养的发展。