思维导图在数学核心素养中的渗透

思维导图在数学核心素养中的渗透

赖静

佛山市南海区盐步职业技术学校

【摘要】思维导图在高中数学教学和学习中有非常重要的地位和作用。无论是在教师的教学中，还是在学生的学习上，都有很大的帮助，思维导图作为一种高效的图形思维工具，能够帮助学习数学有困难的学生减轻负担，激发学生学习数学的兴趣，是培养学生动手能力和自主学习的有效途径。

【关键词】思维导图 核心素养 数学教学 数学学习

【正文】随着中国学生发展核心素养的发布，高考的命题必将进一步注重对学科核心素养的考察，因此作为高中教师，我们必须注意在教学中，加强数学核心素养的渗透。数学六大核心素养包括数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析。

思维导图又叫心智导图，思维导图利用图像和文字将需要记忆、理解、运用的知识点连接起来，针对数学学科特点，利用思维导图进行题型的归类和总结，并且将相应题型的解题思路和步骤写进思维导图，便于学生考前复习时使用，因此它是一种比较高效的图形思维工具。对数学教学和数学学习都有非常重要的作用，在数学核心素养的渗透中具有天然的优势。有许多的研究已经证明思维导图对教师教学及学生自主学习方面有着巨大的优势（见图1）。

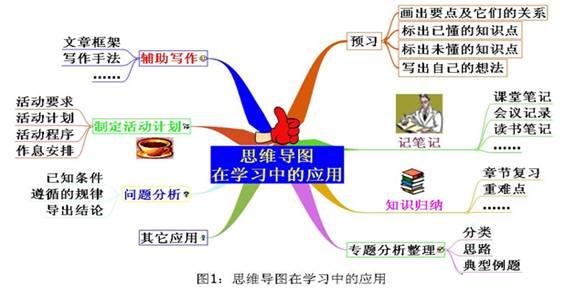
本文针对思维导图在数学核心素养中的渗透进行了一些初步的探讨。

（一）、高中数学跟初中数学相比，要求学生识别并且会使用数学符号，数学语言也比初中抽象；思维导图有助于培养学生的思维整合能力，能够有效解决高一学生的初高中衔接遇见的问题。

作为教师备课是教学必不可少的一项工作，因此如何高效备课一直是教师面临的首要问题，更是我们需要认真研究的问题。

教师备课主要需要考虑几个方面即：1、备教材—首先我们要认真研究课程标准，高考对这个章节知识点的要求；2、备学生—备学生的学习情况和学生在学习过程中或许会遇到的问题以及解决问题的措施办法；备教法—根据备教材和备学生得出的结论，写教学设计，研究整节课的教学方法。

教师利用思维导图将本节课内容利用图文的形式展现给学生，学生在思维导图的的帮助下更容易理清本节课的逻辑关系，更容易理解掌握需要解决的重点、难点内容。比如在《数列》一章的教学设计中采用了思维导图（见图2）。

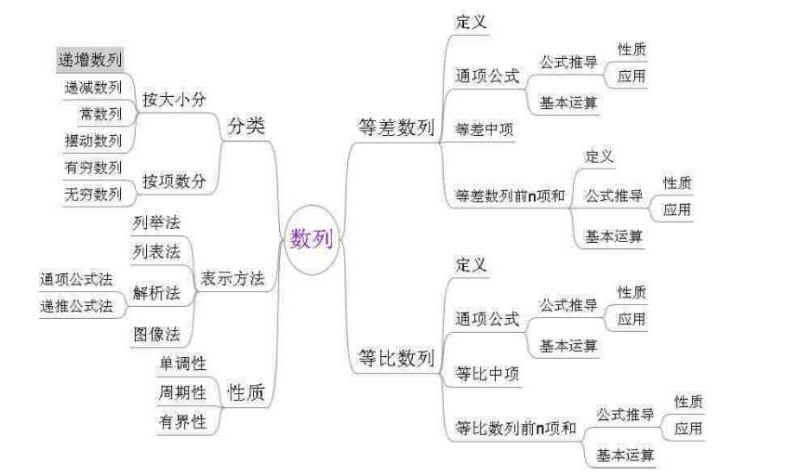
图2《数列》教学设计思维导图

优势在于能够呈现数列的各个知识点之间的联系，帮助对学生形象记忆数列的公式及求通项公式和前n项和的方法步骤。

绘制好每节课的思维导图后，根据实际情况将每节课的思维导图整合连接，就能形成章节思维导图。这样学生可以根据个人需求直接在原来的思维导图上增加或修改，非常方便。这会大大地提高学生的学习效率和质量，从而真正使学习资源达到整合和有效利用的目的。学生在课后需要用某些知识点时，只要脑子里浮现这张思维导图就能直观记起很多知识点和运用该知识点解题时需要注意的地方。

（二）、高中数学知识内容跟初中相比难度加深，课堂容量大，思维导图有利于帮助学生提高课前预习的效率，激发学生主动学习的兴趣,提高数学建模的能力。

数学建模首先要了解研究对象的实际背景，将所要研究的对象用数学语言转换成一个数学问题。数学建模的过程是抽象的，学生容易因为不能理解而产生畏难情绪，甚至是厌学。这首先要求我们要使学生“主动的学习，快乐的学习”，所以我们不能采取“满堂灌”等传统的教学模式，要把课堂还给学生，让学生成为课堂的主体，开展让学生自主探究的课堂模式，运用思维导图开展“自主探究”的课堂模式包含如下几个步骤：

(1)应用思维导图进行课前预习

课前预习是学生自主学习探究问题的重要环节,那么如何提高课前预习的效果是学生面临的一个主要问题,我建议学生利用思维导图进行预习,让他们根据课本绘制自己探究学习过程的思维导图,把每一节的内容总体部分,关键词,各个枝节及其相关逻辑进行整理,让学生自己明确哪些内容已经掌握,哪些还不明白,这样学生就带着问题去听课,可以提高听课的质量。

(2)利用思维导图引入新课，让学生有动手的机会，参与课堂实验中，有助于激发学生的兴趣。

如果我们在新课导入时，创设情境，使用富有启发性的思维导图方式，建立数学模型，可以使抽象问题形象化，更好地调动学生学习主动性，课后更好地总结题型，归纳类型题的解题方法，从而达到更好的学习效果。例如，在讲解椭圆方程的建构时，我选用了如下的方法：

我首先在黑板上给定了两个定点 和一根绳子，请三位同学一起合作完成，先请其中两位同学将绳子的两端分别固定在 上，再请第三位同学用粉笔绷紧绳子并移动粉笔，让同学们观察粉笔运动的轨迹是什么？

当粉笔运动一周后学生观察发现 是定点，M是动点，M运动轨迹是一个椭圆。如下图所示：

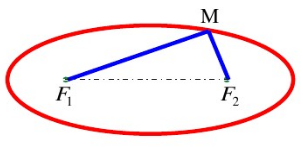
接下来我提示学生思考如下的问题：

1、绳子的两端是否固定？

2、拉紧绳子以后绳子的长度是否产生了变化？

3、绳子的长度和两定点之间的长度有什么关系？假如绳子的长度大于 ，轨迹是什么？假如绳子的长度等于 ，轨迹是什么？假如绳子的长度小于 ，轨迹是什么？

引导思考： ， ，其实2a就是绳子的长度，2c就是 之间的距离，只有 的情况下，绳子运动轨迹才是椭圆。

做完实验后，由学生自己归纳椭圆的定义，教师加以点评和总结。

经过刚才的探究过程，继续引导大家进行思考：想求椭圆的标准方程，必须要先建立适当的直角坐标系，那么哪种方式建立的直角坐标系是最适合的呢？让学生自己想办法建立合适的坐标系（如下图所示）：

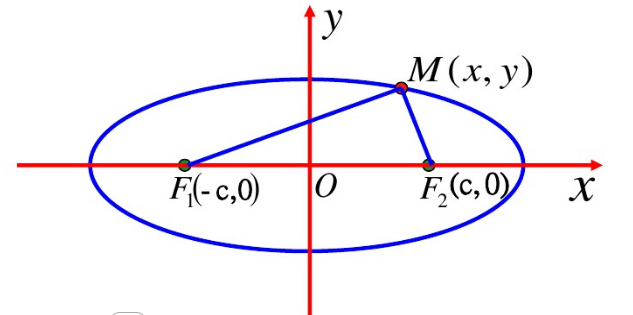
①以 的中点为原点O， 所在直线为x轴，线段 的中垂线为y轴，建立直角坐标系。②设：动点M为椭圆上任意一点，令 =2c（焦距为2c），那么焦点的坐标分别为 （-c，0）， （c，0），由定义得 ，③代入再化简得出焦点在x轴上的椭圆的标准方程。

同理引导学生自己求出焦点在y轴上的椭圆的标准方程。

3. 课后由学生自主完善自己在预习时绘制的思维导图，教师及时归纳和总结学生的思维导图，培养学生创造力。

在课堂上完成对新知识的学习之后，再由学生带着问题整理课堂内容，查找相关的资料，绘制自己的思维导图。在这一环节中作为教师要给予学生相应的指导，引导学生在对整理过程中，梳理知识点，并将整理和梳理的过程写进思维导图中。

思维导图改变了以往传统的做笔记方式，它运用丰富的色彩和图像，将所需要记忆、理解和掌握的知识点和解题思路和步骤形象地展现在思维导图中，改变了传统思维中数学的“枯燥无味”，对学生解决学习数学上的困难有很大帮助，同时也激发了他们学习数学的兴趣。在学生自主探究的过程中，作为教师我们要鼓励学生敢于提出个人想法，激发他们的潜能，提高他们的数学建模能力。

（三）应用思维导图的反思

思维导图作为一种学习的工具和思维方式。虽然在数学教学中有很重要的作用,但是很多学生还是不太习惯思维导图，我们需要在教学过程中慢慢渗透、引导学生学会逐步养成这样的思维方式，让学生慢慢发现思维导图的好处。同时引导学生相互之间经常地交流、学习，效果会更好。

参考文献：

[1] 托尼.巴赞著，张鼎昆、徐克茹译.思维导图—大脑使用说明书[M].北京：外语教学与研究出版社，2005.

[2]王燕．MindManger思维导图在教学中的应用[J]．中国教育技术装备，2007.

第 5 页 共 5 页