渗透“转化”思想观念——“平行四边形面积公式的推导”教学

渗透“转化”思想观念——“平行四边形面积公式的推导”教学

方政文

宁波市 鄞州区首南泰安学校

《数学课程标准（2011年版）》指出：“几何直观主要是指利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要作用。”在小学阶段学生的思维以直观现象为主，逐步向抽象逻辑思维过渡，所以培养学生的空间观念必须符合小学生的心理特征，一般需要经历“直观现象——抽象概括——感性认知——理性认知”等几个阶段。在空间直观教学要注重运用观察、操作、转变、思想等学习方法，注意把握课程目标要求遵循规则设计教学，突出数学知识的本质，切实引导学生在“应用数学”中发展空间观念。

教学内容

新课标人教版数学五年级上册教材第87～88页“平行四边形的面积”教学。

教学目的

1、使学生通过实际操作和讨论思考,探究并掌握平行四边形的面积计算公式,能应用平行四边形计算公式解决相关的实际问题；

2、在数学活动中培养学生观察、分析、概括、推导的能力，发展学生的空间观念，渗透转化的数学思想方法。

教学重、难点

理解平行四边形的面积计算公式推导过程。

教学关键

让学生在动手实践与合作交流中引导学生从不同的途径和方法去探索平行四边形的计算方法。

教学过程

一、动手操作、善于发现

在授课之前教师布置课前预习，要求学生在纸上画出长方形和平行四边形,使长方形的长等于平行四边形的底，长方形的宽等于平行四边形的高,然后再剪出平行四边形和长方形这是为课堂教学备用(基础练习)。因为在三年级上册第七单元学过长方形、四年级上册第五单元学过平行四边形的特征,在本节课教学中教师不必过长时间去复习。因为两个图形的概念在初步认识中已有认知，结合实际要求画一画、剪一剪，我是这样认为,不管学习什么图形,只要学生会画出来的,基本上掌图形的特征,否则难以画出图形。

让学生操作过程善于发现问题。学生在方格纸中画出平行四边形和长方形，要求平行四边形的底等于长方形的长,平行四边形的高等于长方形的宽。先让学生独立思考,观察图形,比较图形面积的大小。然后小组讨论交流,学生把自己的想法与师生交流、反馈。有的学生用剪拼法(图1)；有的数方格(不满一格按半格计算)(图2),都发现了平行四边形的面积和长方形的面积一样大。

图1 图2

二、探究思考、反馈信息

让全班同学交流思考。教师把小组剪去不同的图形进行投影展示, 你是怎样剪拼的,从什么地方剪,为什么这样剪?抛出一些问题, 让全班同学交流思考。通过试错的方法引导学生“为什么一定要从高剪开才能拼成长方形”，让学生明白平行四边形转化长方形的关键。这时师生互动,发挥学生的智慧,开创学生思维空间，让优生带动差生，把错误的剪拼方法挑出来，共同探究修改。正在这时有位学生举手站起来回答出一个重要的信息：平行四边形剪拼必须要从高出发，原因就是拼成后的图形一定要符合长方形的特征；接着教师提出一个问题，进一步引导学生，如果不从角的垂线去剪而从上下边垂线去剪，能拼成长方形吗?学生又一次交流、探讨,促使他们发现了：平行四边形中有无数条高，只要从图形的高剪出都能拼出长方形。通过全班交流，教师引导学生归纳：这个长方形的长与平行四边形的底相等，长方形的宽与平行四边形的高相等，交流引导、归纳：平行四边形面积公式：“底×高”。

结合反馈信息本节课的教学知识点，展示教学中的研讨题：

(一)把长方形拉成平行四边形结果会怎样?

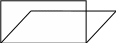
①面积、周长都相等。②周长相等，面积变了。③面积相等，周长变了。

开展小组讨论、交流,可以借助学具操作演示。汇报时答案可能不一样,这时教师引导、开发学生的思维能力和观察能力,把事先准备好的活动长方形框架附上黑板让几位小组长上台演示。教师向学生提出问题,通过你们的观察后有发现什么呢?师生共同交流,部分学生找到结果,拉成平行四边形时底没有改变,而宽变成平行四边形的斜边。平时很多学生误把斜边当作高求面积,从而让学生有点反思,得出正确答案应是第②种答案。

(二)在平行线间画出同底平行四边形,发现什么？

先让学生独立思考，并在小组中交流想法，然后教师组织学生进行全班交流。学生第一个发现问题是这两个平行四边形的底相同(同底),在老师的引导下，学生很快发现第二个问题是平行线间距离处处相等,可以反映这两个平行四边形的高相等(等高)。最后师生得出结论:等底等高的平行四边形的面积相等。

三、渗透转化、提升观念

在图形教学中，加强学生动手实践，自主探索，使学生得到较多的有关空间观念的训练机会。例如：学习平行四边形的面积这节课是先借助数方格的方法，再引导学生通过剪一剪、拼一拼的操作过程，将平行四边形转化为长方形,推导平行四边形的面积计算方法。

对平行四边形的面积教学感想：

1.重视动手操作与实践

“平行四边形的面积”的教学，是学生第二次接触图形面积，从平行四边形的面积开始，学生不在只会利用格子图的方法推导面积计算公式，而是提升为运用转化研究图形之间的联系来推导面积计算公式。在推导过程中教师即要做好引导,又要注意不要包办代替,要求学生在独立思考和合作交流的基础上进行操作,切忌由教师带着做，其目的是发展学生的空间观念和操作能力。

2.引导学生探究,渗透“转化”思想

“转化”是数学学习和研究的一种重要思想方法。“平行四边形的面积”这节课的核心是转化思想，转化思想是研究和解决问题的一种有效思考方法。通过操作，一方面启发学生设法把研究的图形转化为已经会计算面积的图形，滲透“转化”的思想方法；另一方面引导学生去主动探究的图形与转化后的图形之间有什么联系，从而找到面积的计算方法,切忌由教师直接演示讲给学生。利用讨论和交流等形式,要求学生把自己操作——转化——推导——应用的过程叙述出来,以发展学生的思维和表达能力。

3.培养学生用多元化解决问题的能力

教师以自己试错的方法帮准学生理解沿着平行四边形的高剪开才能拼成长方形的关键，然后让学生发现平行四边形有无数条高，把学生的思考引向深处，进一步发展学生的数学思维和空间观念。在运用转化的方式推导面积计算公式和计算多边形面积,可以有多种途径和方法，教师注意不要把学生的思维限制在一种固定或简单的途径或方法上,要尊重学生的想法,鼓学生从不同的途径和角度去思考、探索解决问题的兴趣及发现。